Validité d'un algorithme

Objectif

  • Comprendre la notion de validité d'un algorithme.

Mise en situation

L'usage des algorithmes est devenu massif et il est primordial de toujours s'assurer, voire de prouver que son algorithme est valide afin que son utilisation ne pose aucun problème.

Prouver un algorithme

Il est possible de fournir deux preuves mathématiques montrant qu'un algorithme est correct : une preuve d'arrêt et une preuve de validité.

La preuve d'arrêt assure que l'algorithme s'arrêtera forcément à un moment, c'est-à-dire qu'il n'y a pas de cas où il entrerait dans une boucle infinie.

La preuve de validité assure que le résultat est bien celui visé, que le but de l'algorithme est atteint quelles que soient les données d'entrée.

ConseilPlus facile à dire qu'à faire...

Ces preuves sont souvent très complexes et ne sont pas nécessaire dans un usage quotidien. Un développeur utilise la plupart du temps des algorithmes simples ou de légères adaptations d'algorithmes connus et déjà prouvés. Ces preuves sont nécessaires essentiellement dans le milieu de la recherche en informatique ou pour des applications très critiques, comme dans un logiciel de contrôle de fusée.

ComplémentComment prouver un algorithme

La logique de Hoare est le formalisme le plus répandu pour réaliser les preuves de validité et d'arrêt.

DéfinitionValidité

Un algorithme est considéré comme valide si le résultat renvoyé est le bon pour toute entrée possible. Il est donc important de bien spécifier le domaine de définition des entrées. Si une entrée est un nombre, il faut préciser si c'est un entier, un entier positif, un réel, etc. Un algorithme donné pourrait fonctionner avec des entiers seulement et il est important que cela soit précisé afin que l'algorithme soit considéré comme valide.

MéthodeVérifier empiriquement la validité

Bien qu'une preuve formelle ne soit pas nécessaire, il est possible très simplement de vérifier la validité. Pour ce faire, il faut vérifier la validité pour quelques valeurs classiques et des valeurs dites extrêmes.

ExempleExemple de vérification empirique

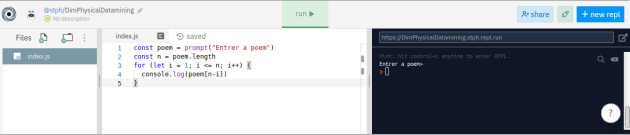
L'algorithme ci-dessous récite le poème donné à l'envers. Les valeurs classiques seront des chaînes de caractères non vides. La valeur extrême à tester est une chaîne de caractères vide.

Après avoir vérifié ces cas, le développeur est assuré assez fortement de la validité de son algorithme.

1
Entrée:
2
    poème, chaine de caractère
3
4
n = longueur(poème)
5
Pour i de 0 à n-1 alors:
6
    Afficher poème[n-i]
7
FinPour
1
const poem = prompt("Entrer a poem")
2
const n = poem.length
3
for (let i = 1; i <= n; i++) {
4
  console.log(poem[n - i])
5
}
6
ComplémentValidité et tests unitaires
Dans un contexte professionnel, un développeur peut mettre en place des tests unitaires automatisés qui permettent de vérifier empiriquement la validité de l'algorithme à chaque modification du code.
À retenir
  • Un algorithme est valide s'il retourne toujours le résultat attendu pour toutes les entrées possibles.
  • Il est possible de vérifier empiriquement la validité en exécutant l'algorithme pour quelques valeurs précises notamment les valeurs extrêmes.