Exercice : Appliquer la notion
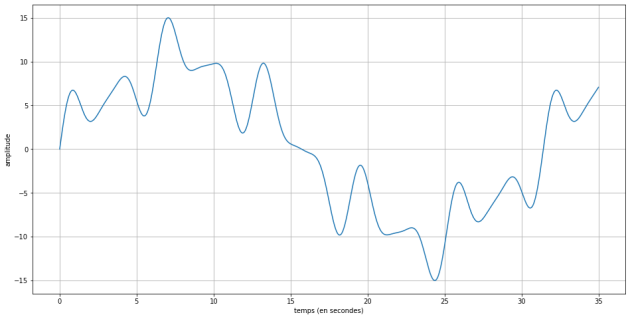
On se donne la plage suivante d'un signal analogique observé.
Généré avec python
```python
import matplotlib.pyplot as plt
import numpy as np
x = np.linspace(0, 35, 1000)
y = 3 * np.sin(2 * x) + 2 * np.sin(1 * x) + np.sin(3 * x) + 10 * np.sin(0.2 * x)
plt.figure(figsize=(16,8))
plt.grid(which='major', axis='both')
plt.ylabel("amplitude")
plt.xlabel("temps")
plt.plot(x,y)
```
Question
On souhaite le discrétiser. Pour cela, on choisit de prendre des échantillons de ses valeurs toutes les 5 secondes en prenant la première valeur à l'origine.
Combien d'échantillons va-t-on récolter avec cette plage du signal observé ?
Solution
On obtient 8 valeurs du signal aux temps : 0, 5, 10, 15, 20, 25, 30, 35.
Question
On souhaite maintenant numériser les valeurs de ces échantillons au multiple de 5 inférieur le plus proche.
Quelles sont, dans l'ordre, les valeurs entières associées ?
Indice
Par exemple, 0 est le multiple de 5 inférieur le plus proche de 0.3 mais aussi de 0.0.
De même, -5 est le multiple de 5 inférieur le plus proche de -2.1 et de -4.00001
Solution
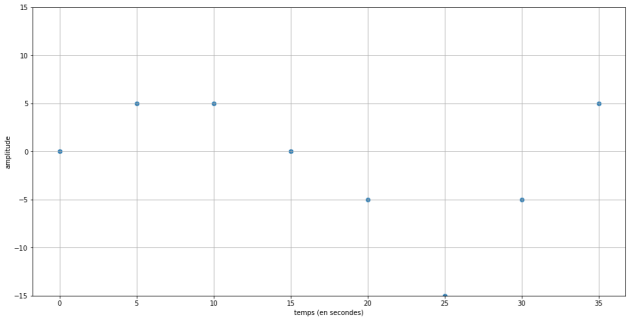
On obtient après la discrétisation et la numérisation le signal suivant :
Généré avec python
```python
import matplotlib.pyplot as plt
import numpy as np
x = np.linspace(0, 35, 8)
y = 3 * np.sin(2 * x) + 2 * np.sin(1 * x) + np.sin(3 * x) + 10 * np.sin(0.2 * x)
plt.figure(figsize=(16,8))
plt.grid(which='major', axis='both')
plt.ylabel("amplitude")
plt.xlabel("temps (en secondes)")
plt.ylim(-15,15)
plt.scatter(x,y // 5 * 5)
```
On obtient les valeurs suivantes : 0, 5, 5, 0, -5, - 15, -5, 5.
Question
Cette représentation discrète n'est pas très bonne car elle ne prend pas suffisamment en compte les variations des valeurs du signal.
Quels sont les deux paramètres sur lesquels on peut agir pour améliorer la discrétisation ?
Solution
On peut réduire la période temps (appelée période d'échantillonnage) de 5 secondes à par exemple 1 seconde. En augmentant le nombre de données échantillonnées, on se rapproche de plus en plus du signal initial.
On peut également augmenter la résolution du signal échantillonné, par exemple en numérisant les valeurs à l'entier inférieur le plus proche. Ainsi on se rapproche de plus en plus des valeurs échantillonnées.