Automates et diagramme états-transitions
Impossible d'accéder à la ressource audio ou vidéo à l'adresse :
La ressource n'est plus disponible ou vous n'êtes pas autorisé à y accéder. Veuillez vérifier votre accès puis recharger la vidéo.
Transcription textuelle
Objectifs
Découvrir ce qu'est un automate ;
Savoir lire un diagramme de transition.
Mise en situation
Le concept de machine de Turing s'inscrit au sein de la théorie des automates. Un automate est un dispositif qui est capable de produire une série d'actions sans intervention humaine. Il est programmé pour produire ces actions. Une horloge est un exemple d'automate simple.
Un ordinateur est un automate qui est capable de recevoir plusieurs programmes différents. Il peut effectuer des actions très diverses, pas seulement donner l'heure, grâce à des périphériques puissants, comme l'écran.
Fondamental : Théorie des automates
Un automate est un modèle mathématique permettant de réaliser des calculs, composé de plusieurs états. Le passage d'un état à un autre est conditionné par les données transmises à l'automate.
Fondamental : Diagramme états-transitions
Un diagramme états-transitions permet de représenter les états d'un automate et les passages possibles d'un état à un autre.
Un état est représenté par un nœud (un cercle).
Un changement d'état est modélisé par une flèche accompagnée de la condition de ce changement.
Il est possible qu'une flèche pointe sur l'état dont elle vient lorsqu'une action ne modifie pas l'état.
Exemple : Automate très simple
Un portillon possède deux états : verrouillé et déverrouillé. On comprend que pousser une porte verrouillée ne la débloque pas mais qu'insérer un jeton si.

Remarque : Machine de Turing et automate
Une machine de Turing est un type avancé d'automate : le passage d'un état à un autre est conditionné par le symbole lu sur le ruban.
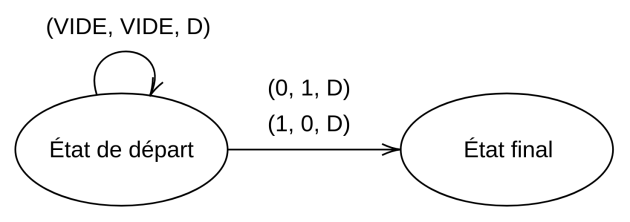
Méthode : Comment lire le diagramme états-transitions d'une machine de Turing ?
Une machine de Turing étant un automate très particulier, son diagramme possède une particularité : la condition de changement d'état.
La condition de changement d'état est représentée par un triplet :
([symbole lu] ; [symbole écrit] ; [déplacement])
Exemple : la condition (1; 0; D) signifie que si la tête lit le symbole 1, il faut écrire le symbole 0 puis déplacer la tête de lecture/écriture vers la droite.
Exemple : Machine très simple
À retenir
Une machine de Turing est un type d'automate.
Il est possible de représenter une machine de Turing grâce à un diagramme états-transitions.
Impossible d'accéder à la ressource audio ou vidéo à l'adresse :
La ressource n'est plus disponible ou vous n'êtes pas autorisé à y accéder. Veuillez vérifier votre accès puis recharger la vidéo.